Computing the total of a bill, taking Service Charge and 12% VAT into account is a common task that software engineers or spreadsheet developers may have to do.
Let's say you, for some unfortunate reason, have to compute how three people will split a restaurant bill, including VAT and Service Charge. You read "What Every Computer Scientist Should Know About Floating-point Arithmetic" then, applying the lessons there, do one of the following:
- Store and compute amounts in cents
- Use a decimal data type (instead of floating-point)
- Use an infinite-precision data type
And assume that the issue is fixed. Then fast-forward a few days (or weeks) later, finance calls you and informs that their computations do not match yours, and that you're off by a cent in a couple of areas. What's happening?
It's important to note that monetary arithmetic is case-specific. This means that even when using error-minimizing numerical representations, you still need to be aware of how the values are used in your case when implementing operations. Similar cases like this include:
- Splitting a ₱100 bill between three friends.
- Doing a 70-30 revenue split between the agents and the company.
- Converting ₱2499.99 (PHP) to USD.
Motivating Example: Bill Splitting
Let roundc(x) be a function that rounds x to the nearest cent. So ₱100.105 will get rounded to ₱100.11.
To make the problem easier, we'll focus on splitting the bill as an example: ₱100 divided by 3 is ₱33.333... the first step is knowing that it's more important that the sum is still 100 rather than getting an exact equal split. So a naive solution of computing roundc(₱100/3) = ₱33.33 for all parties is wrong because if you add the value up, it will be ₱99.99 rather than ₱100. Note that if you use an infinite-precision data type, your countercheck (₱33.333... + ₱33.333... + ₱33.333... = ₱100.00) will fail to detect this error if you don't round it to what is being displayed (₱33.33 rather than ₱33.333...) when counter-checking.
The result of this error will then again be dependent on the case. If this algorithm is part of an automated system that processes 1,000 transactions per day, then that's a loss of ₱10 per day (note that the accumulation depends on the volume of transactions, not on the magnitude per transaction). While percentage-wise, it might not be much, many businesses still care about the absolute value and the value goes up the higher the value of the base currency is (imagine of we operate on Euros rather than Philippine Pesos).
If it's just a utility mobile app, then hope that your users are smart enough to decide who pays the additional cent or the restaurant they are in would just waive the cent. In this case though, an alternative is to have everyone pay ₱33.34 and put the spillover as part of the tip.
Note that in this case (and also in other cases), using an infinite precision number, does not fix the problem. In this instance, additional decisions need to be made on when the rounding happens, and where to channel unavoidable excesses or discrepancies as a result of calculations.
Reason
These issues arise mainly because of two things:
Monetary value is a finite-precision decimal
We stop at a certain precision level (usually cents) because we use base 10 for counting and computation as opposed to continued fractions or rational numbers and that "physical" space is limited when writing down those numbers. Imagine how your grocery receipt will be if the amounts are written in fractions. This limitation is not because currencies are old. In fact, Bitcoin also has a precision limit: the smallest bitcoin unit is a satoshi which is one millionth of a Bitcoin. So one could say that using infinite-precision numbers is an approximation of finite-precision monetary amounts!
An exception proving this rule is FOREX, microchips, AWS EC2 pricing, and things that are usually sold/exchanged in bulk. For example, for FOREX, sure it's more than 2 decimal places (1 JPY = 0.4416 PHP), but if you wanna do the actual conversion, there's a minimum amount! You can't just go to a FOREX and trade exactly 1 JPY for PHP: they usually have a minimum amount and can only trade in multiples of that amount (e.g. can only trade per 1000 JPY). Moreover, the reverse exchange rate (PHP → JPY) rate is not the reciprocal (computing 1/x) of the JPY → PHP rate but an entirely different measure altogether (but it's usually used as a rough baseline estimate) so there's no direct need to compute 1/0.4416 with high precision.
Other goods sold in bulk follow the same pattern, like the 555 timer, although the unit price's precision is less than a cent ($0.09551), one cannot just buy 1, but will have to purchase at least 6,000 of them (the Minimim Order Quantity).
Certain operations "generate" precision
Remember in grade school when you were taught division and the remainder was introduced? This then led into fractions and decimals. In other words, division can generate additional information that cannot be represented with the data type of the operands (an integer divided by an integer can result in not an integer).
While division is the only operation that can generate precision, there are ways where it can sneak in like multiplication by a fraction and exponentiation. As such, it's more helpful to whitelist operations that do not generate precision. They are:
- Addition
- Subtraction
- Multiplication by an integer
- Division by a divisor (e.g. 12 divided by 6, 2, or 3)
Those familiar with floating-point operations would notice that subtraction is present! While it's true that subtraction generates errors ("loss of significance" is the accurate term) in floating-point numbers, the same does not hold for fixed-point because fixed-point is an exact representation, unlike floating-point (i.e 0.1 is 0.1, not 0.100000001490116119384765625).
The two reasons above are at odds with each other
If all the operations we do does not generate precision, then finite precision is no problem at all. If we use fractional representations, then operations that generate precision will not be a problem unless you use transcendental functions (which produce irrational numbers that cannot be represented by a fraction).
Unfortunately, division is a common operation when dealing with money like splitting bills in the first example. It also arises when computing for discounts and markups. Exponentiation of money appears when computing interest in financial instruments (loans, investments, and derivatives).
Solution
How do we solve the problem? Unfortunately, as illustrated in the example, using a better data type does not solve the problem completely.
Fortunately, there are two rules and two guidelines to follow. They are relatively easy to understand and does not involve complex math (though number literacy is needed) so you do not need to know Kahan Summation or some complex algorithms in order to understand them.
Rule 1: What's displayed is the truth.
The moment you display the number to the user, that displayed number becomes the truth, not the original number that was rounded to what was displayed. For example, if you have total = 12.354915 then you show it to the user as "Total: 12.35", the value of total should then be 12.35 exactly (i.e. 12.35 replaces 12.354915 as the real value) and should be used for the rest of the calculations (e.g. 12% VAT should be computed against 12.35 instead of 12.354915).
This rule seems easy enough but require diligence to follow: every number that a product manager (or government regulator) requires you to show, will be a number that gets replaced with its rounded value. It's very easy to just show the number without revisiting the calculations.
For instance, when working with spreadsheets (e.g. Excel), it is not enough to format the number: the rounding has to be included in the formula themselves. Drake here will show an example:
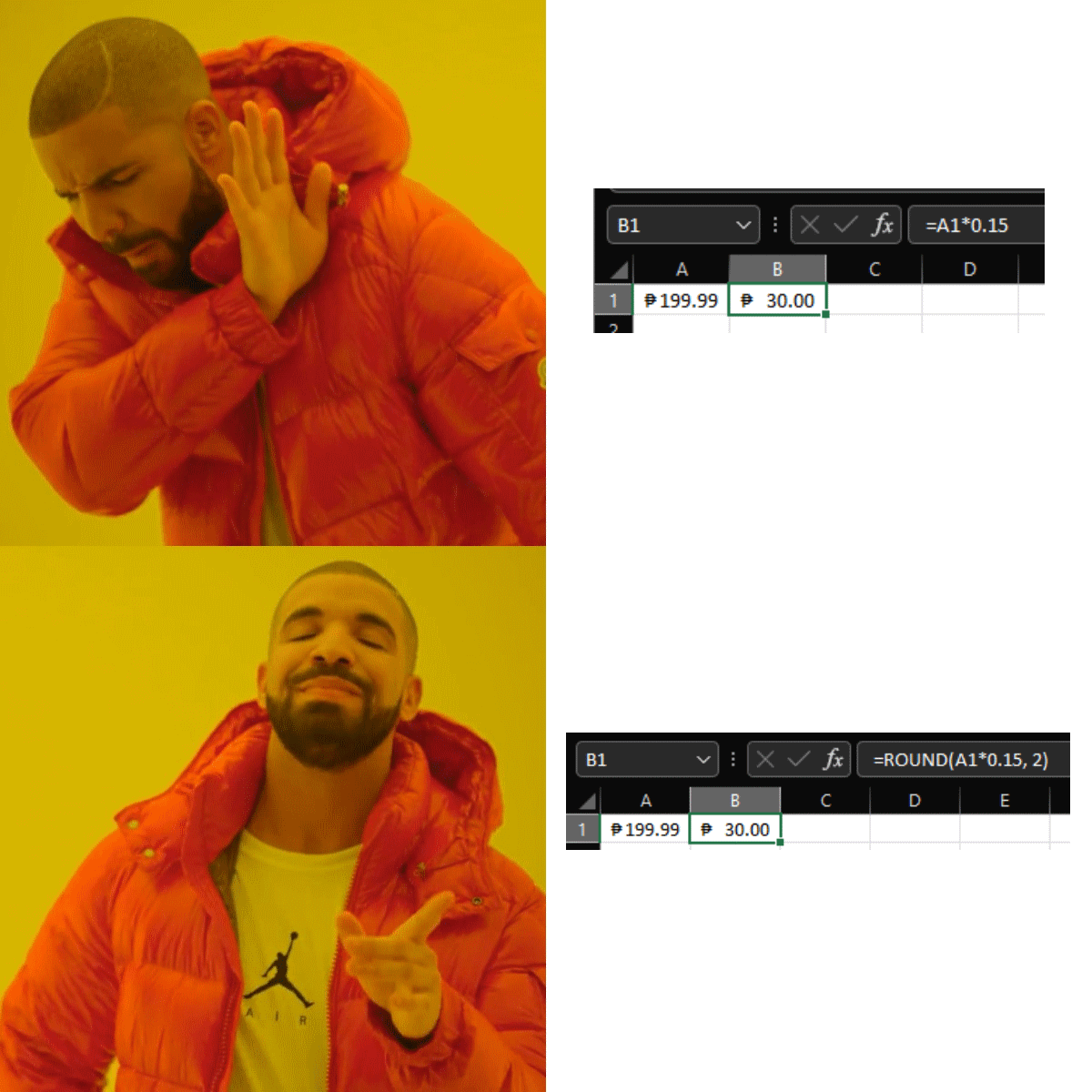
Why this rule? It's because what you show the user is the value that's going to be used, not that highly-accurate, infinite-precision number stored in memory. They will see 12.35 and copy that number to their reimbursement form, their tax forms, insurance claims, etc. they won't be bothering with 12.354915.
Rule 2: Splitting should sum up to the original.
If the division is a splitting, adding the parts should give you the original value. While obvious, this becomes tricky to implement especially with the context of the previous rule. The first example illustrates this perfectly: 100/3 = 33.3333... and applying Rule 1, the actual value becomes 33.33. However this rule requires us to counter-check: 33.33 + 33.33 + 33.33 = 99.99; we are missing one cent! Where that cent goes is up to you or the product manager (see guidelines below) the important point of this rule is the awareness that discrepancies like this may exist!
A common (but not the only) way to resolve this is to make one value the difference of the original and the total of the other values. Mathematically speaking, if T is split into p1, p2, ..., pn, then instead of computing pn directly, you compute pn = T - (p1 + p2 + ... + pn-1) instead.
For example, 52.15 is to be split 70-30, instead of 52.15 × .70 = 36.51 and 52.15 × .30 = 15.65, (36.51 + 15.65 = 52.16 we are over one cent), we just compute the 30 split as 52.15 - 36.51 = 15.64.
Here are some cases to watch out for this rule:
- Splitting a pool of money: As previously explained (the sum of the split must be equal to the original value). This applies to all splits, not just even ones (e.g. 70-30 split of App Stores).
- Discounts: the discounted price plus the discount amount should equal to the original price.
- Pre-tax values: VATable sales plus VAT should equal to the VAT-inclusive price.
Guideline A: Know which values are magnified.
Where should the missing (or extra) cent go? One aspect that can help with the decision is knowing which values are magnified. In many cases, there is asymmetry on the volume of transactions: like how a customer may buy from a store at most once a week but the store processes hundreds or even thousands of transactions per day. So the effect of a discrepancy in calculations is more magnified in one than the other.
For example, suppose from a computation, an extra cent will have to go somewhere and we have to decide whether it should go to the customer or to the store. A customer paying an additional centavo would mean almost nothing for them because even if they buy stuff from your store everyday, they'll lose 3.65 PHP per year. Compare this if the store pays for the extra centavo instead, if they receive 100 customers per day, then they will end up losing 365 PHP per year. In this case the one centavo's effect is magnified more for the store than for the customer.
This does not automatically mean that the loss should be shouldered by the customer, but it does elaborate the effects of decisions. More often than not, these decisions are judgements that may need to be propagated to management, especially if regulations are involved (what if we're referring to tax instead?)
Guideline B: Sometimes, predictability is better than accuracy.
Reaching for the round function all the time might be tempting because it's the most "accurate". However, rounding down or up might be better in some cases because their error is more predictable:
roundup(x) ≥ xall the time, androunddown(x) ≤ xall the time.
Compare it with round function which, does not have such guarantees (it can be greater or less than the original value). When would rounding up or down be better? Here are some cases:
- Computing taxes (better overpay than underpay by a centavo and get chased by the tax authorities who happen to round things differently)
- Automatically favoring a party in a split (for example, company doing a 70-30 revenue split will round down the other party's split in order to favor theirs)
- Making the error residuals always positive (or negative) when enforcing Rule 2. For example, when doing an even split like 200/3, a round down would always result in a positive residual (200 - 66.66 × 3 = 200 - 199.98 = 0.02 > 0; a round would result in an overestimation).
Application: Proportional Bill Split with Service Charge and VAT
To illustrate how the rules and guidelines are applied, we compute the bill of three friends eating at a restaurant, taking into account the service charge and VAT, and how much would each pay if they decide to split the bill. Here are the important points:
- They agree to pay for their own meal.
a. Friend A: ₱159.94
b. Friend B: ₱174.99
c. Friend C: ₱129.99 - But they buy a pitcher of iced tea (₱100), which they agree to split equally.
- There is a 12% VAT applied to sales.
- There is a 10% Service Charge based on VAT-inclusive price that's not subject to VAT [1].
- Prices are VAT-inclusive, but exclusive of service charge.
- The reciept has the following fields printed:
a. Item Price (VAT-inclusive)
b. Subtotal
c. Service Charge
d. Grand Total
e. VATable Sales
f. VAT
We first compute what should be printed on the receipt:
- The Subtotal is straight forward, just add
₱159.94 + ₱174.99 + ₱129.99 + ₱100.00 = ₱564.92 - For the 10% service charge, we round up to favor the store (Guideline A & B) so
roundupc(₱564.92 × 10%) = ₱56.50. - The Grand Total is
₱564.92 + ₱56.50 = ₱621.42. Note that we didn't compute it as₱564.92 + 10%because of Rule 1. - Compute the VATable sales as Subtotal / 12% and we round down (Guideline B; explanation in the next point). So
rounddownc(₱564.92/1.12) = ₱504.39. - Compute the VAT as
₱564.92 (Subtotal) - ₱504.39 (VATable sales) = ₱60.53. No rounding is needed because we are just subracting. Note that we are not computing it as VATable sales + 12% due to Rule 2, moreover, due to the rounding down in the previous step, we are actually very slightly overpaying the VAT.
Computing the split between friends is trickier: we first have to factor in the service charge to each item, then split the price of the drink, service charge included, proportional to the order amount of each friend.
There are two ways to compute the price of each item with the included service charge:
- Spilt the service charge proportionally per item, or
- add the 10% service charge per item.
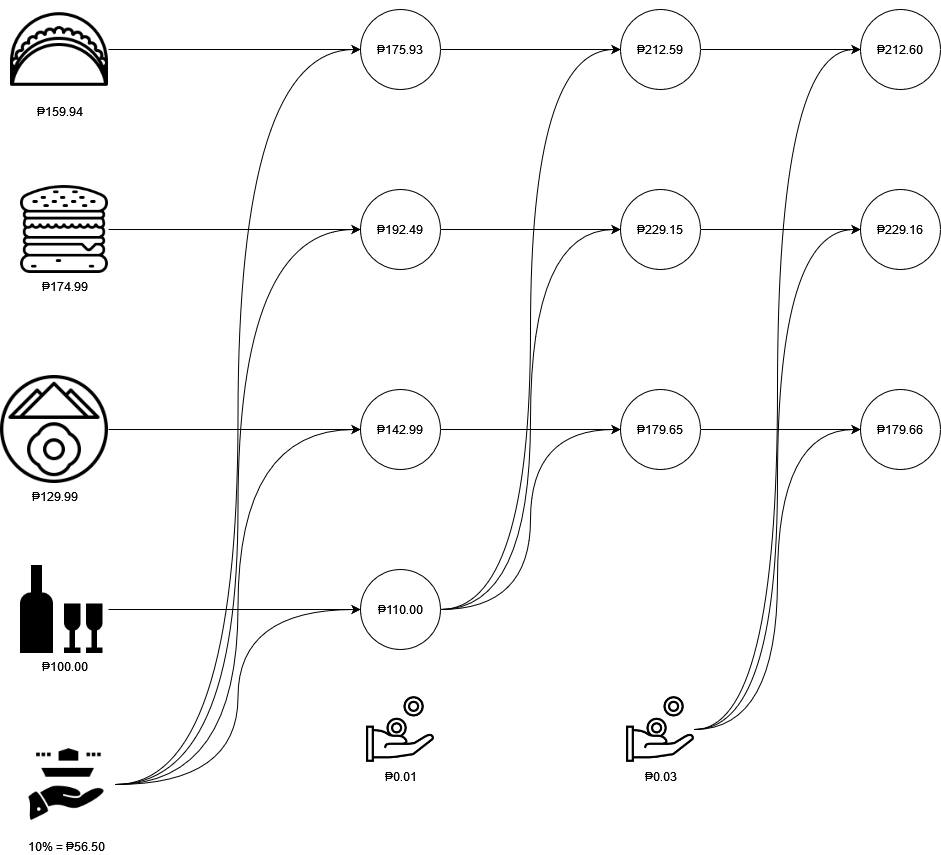
we will go with (2) for its simplicity. So for each item, we compute roundc(x × 1.10) and note the deviation of their sum from the Grand Total ₱621.42 (Rule 2):
- Friend A: ₱159.94 → ₱175.93
- Friend B: ₱174.99 → ₱192.49
- Friend C: ₱129.99 → ₱142.99
- Drinks: ₱100.00 → ₱110.00
The total is ₱621.41 which off by one centavo but we don't distribute it yet since we still have to split the price of the drink ₱110.00. For the drink split, we use Guideline B and roundownc(₱110.00/3) = ₱36.66. So the spilt is now:
- Friend A: ₱175.93 + ₱36.66 = ₱212.59
- Friend B: ₱192.49 + ₱36.66 = ₱229.15
- Friend C: ₱142.99 + ₱36.66 = ₱179.65
Counter-checking due to Rule 2, the sum (₱212.59 + ₱229.15 + ₱179.65) is ₱621.39, which is off by 3 centavos, which we just distribute equally. So the final split amount for each friend is:
- Friend A: ₱212.60
- Friend B: ₱229.16
- Friend C: ₱179.66
Here's a diagram to aid in understanding where the amounts flow.
The computations in Google Sheets can be accessed here.
Closing Remarks
Monetary amounts require a bit more nuanced handling than ordinary fixed-precision number. One thing to keep in mind is like matter, money does not magically increase or decrease when you perform transactions (unless we are talking about interest). The rules and guidelines discussed help rationalize the choices we make when performing calculations with them.
Computations like these come up in our projects from time to time (one being the Service Contracting Program) and it's something that we pay close attention to using the rules and guildelines discussed.
If you’ve found this interesting or helpful at all:
- I’m glad!
- Drop us a line and let us know!
- Consider working with us! Sakay’s tech team tends to focus on transport and mapping, but as you can see, we tend to go a bit wide.
P.S.: This blog post is inspired by https://blog.xendit.engineer/benchmarking-pg-numeric-integer-9c593d7af67e head over there to know the tradeoffs in representing monetary arithmetic in PostgreSQL!
Is the service charge subject to VAT? For Philippine context, see RMC 29-70 (issued in 1970), printed in the Philippine Taxation Encyclopedia which states that service charges are not subject to VAT as long as they are given to staff and not management. There's a separate bill, RA 11360 signed on 2019 which mandated that 100% of the service charge should go to staff. So in effect, service charge (despite its name) is not subject to VAT even if it's non-discretionary.
However, there is no rule on how the service charge should be computed. Percentage-based service charge can be based off the VAT-inclusive or VAT-exclusive price: it depends on the establishment. I've seen restaurants compute the service charge with either price. ↩︎
