Given a list of numbers, there are multiple ways of computing the average and variance (including the standard deviation). A blog entry by Dr. Cook outlines various ways computing them, as well as their characteristics.
One particular method that I would like to focus on, is the iterative method detailed here. It's a wonderful algorithm that requires only \(O(1)\) space for computing the average and variance even if entries come in one at a time. I first encountered this method when studying under Dr. Kardi Teknomo and was enamored by its utility and simplicity.
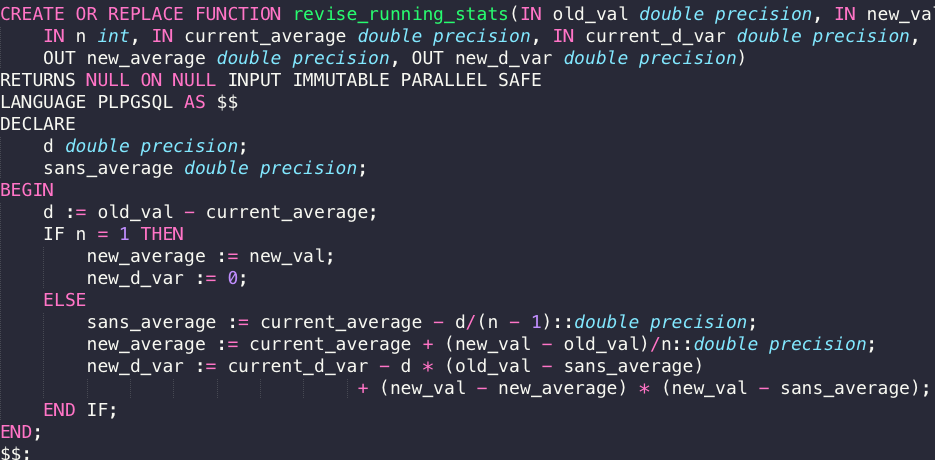
In implementing systems using those methods, we came upon the requirement that the average and variance should be updated in response to entries being revised (a new value replaces the old) or deleted. Moreover, it would be preferred if it could be done incrementally using only \(O(1)\) space like the original method.
Below are the formulae for doing such. A reasonable requirement for the formulae is that the value to be deleted or revised should be known, as well as the current count, average, and "denormalized" variance (sum of squared difference from the mean, same as the \(S_k\) term in Dr. Cook's article). These formulas are really handy when using SQL triggers to update averages and variances.
Deleting Values
Where:
- \(x_k\) is the value to be deleted,
- \(k\) is the current number of elements,
- \(M_k\) is the current average,
- \(S_k\) is the current "denormalized" variance,
- \(M_{k-1}\) is the new average with \(x_k\) deleted, and
- \(S_{k-1}\) is the new "denormalized" variance with \(x_k\) deleted.
The formula for computing \(M_{k-1}\) and \(S_{k-1}\) is:
$$\begin{aligned}d &= x_k - M_k\\ M_{k-1} &= M_k - \frac{d}{k - 1}\\ S_{k-1} &= S_k - (x_k - M_{k - 1})d\end{aligned}$$
Updating Values
Where:
- \(x_k\) is the old value
- \(x_n\) is the new value that replaces \(x_k\)
- \(k\) is the current number of elements,
- \(M_k\) is the current average,
- \(S_k\) is the current "denormalized" variance,
- \(M_n\) is the new average with \(x_k\) replaced by \(x_n\), and
- \(S_n\) is the new "denormalized" variance with with \(x_k\) replaced by \(x_n\).
The formula for computing the \(M_n\) and \(S_n\) is:
$$\begin{aligned}d &= x_k - M_k\\ M' &= M_k - \frac{d}{k - 1}\\ M_n &= M_k + \frac{x_n - x_k}{k}\\ S_n &= S_k - (x_k - M')d + (x_n - M_n)(x_n - M')\end{aligned}$$
Derivation
The above formulae are derived by simple algebra. Let \({x_k}\) be a sequence of length \(k\). Without loss of generality, the value to be deleted is the last value, \(x_k\), the average \(M_{k-1}\) with \(x_k\) removed can be computed from the formula for adding \(x_k\):
$$\begin{aligned}M_k &= M_{k-1} + \frac{x_k - M_{k-1}}{k}\\ kM_k &= kM_{k-1} + x_k - M_{k-1} = (k - 1)M_{k - 1} + x_k\\ M_{k-1} &= \frac{kM_k - x_k}{k - 1} = \frac{kM_k - M_k + M_k - x_k}{k - 1}\\ M_{k-1} &= M_k - \frac{x_k - M_k}{k-1}\end{aligned}$$
\(S_{k-1}\) is easily derived from the addition formula, given that we already know \(M_{k-1}\):
$$\begin{aligned}S_k &= S_{k-1} + (x_k - M_{k-1})(x_k - M_k)\\S_{k-1} &= S_k - (x_k - M_{k-1})(x_k - M_k)\end{aligned}$$
The update formulas are derived by applying the addition formula again:
$$\begin{aligned}M_n &= M_{k-1} + \frac{x_n - M_{k-1}}{k}\\&= M_k + \frac{x_n - x_k}{k} \\ S_n &= S_{k-1} + (x_n - M_{k-1})(x_n - M_n)\\ &= S_{k} - (x_k - M_{k-1})(x_k - M_k) + (x_n - M_{k-1})(x_n - M_n) \end{aligned}$$